Abstract
기본적으로 $O(N^2)으로 정렬하는 알고리즘(Ex : 버블 정렬, 선택 정렬, 삽입 정렬)바꾸는 기준이 순회흘 하면서 바뀌며, 일반적으로 for문의 중첩으로 $O(N^2)의 복잡도를 가지게 된다. 하지만 퀵 정렬 알고리즘은 직관적으로 보았을 때, 비교를 반씩 줄여나가면서 정렬하는 알고리즘으로 즉, 재귀를 이용한 분할정복 알고리즘이다.
- 분할(Divide) : 입력 배열을 피벗을 기준으로 비균등하게 2개의 부분 배열(피벗을 중심으로 왼쪽: 피벗보다 작은 요소들, 오른쪽 : 피벗보다 큰 요소들)로 분할한다.
- 정복(Conquer) : 부분 배열을 정렬한다. 부분 배열의 크기가 충분히 작지 않으면 순환 호출을 이용하여 다시 분할 정복 방법을 적용한다.
- 결합(Combine) : 정렬된 부분 배열들을 하나의 배열에 합병한다.
- 순환 호출이 한번 진행될 때마다 최소한 하나의 원소(피벗)가 최종적으로 위치가 정해지므로, 이 알고리즘은 반드시 끝난다는 것을 보장할 수 있다.
Process
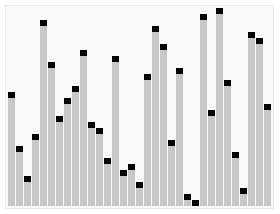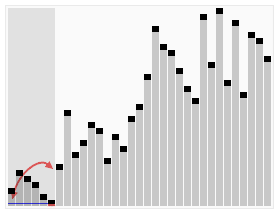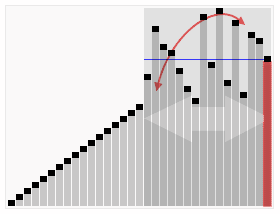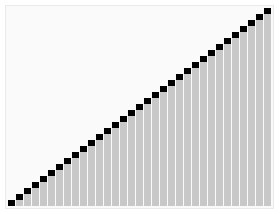
- 특정한 기준을 통해 Pivot 값을 지정한다.(먼저 아래 코드와 설명에서는 가장 앞의 값을 기준으로 잡겠습니다.)
- Pivot을 기준으로 작으면 왼쪽으로, Pivot보다 크면 오른쪽으로 이동한다.
- 이동하는 방식은
- Pivot 위치를 고정하고 왼쪽에 있는 값들을 다시 1번부터 실행, 오른쪽에 있는 값들을 1번부터 실행한다.
- 양쪽 값이 1개인 경우 멈추게 된다.
Python Code
def quickSort(arr:list):
def recursion(temp:list):
if len(temp) == 1 or len(temp) == 0: # 6.
return temp
pivot_idx = 0 # 1.
pivot = temp[pivot_idx]
low = pivot_idx + 1
high = len(temp) - 1
low_change, high_change = False, False
while high > pivot_idx and low < len(temp) and low <= high: # 2.
if temp[low] < pivot:
low += 1
else:
low_change = True
if temp[high] > pivot:
high -= 1
else:
high_change = True
if low_change and high_change: # 3.
temp[low], temp[high] = temp[high], temp[low]
low_change, high_change = False, False
temp[pivot_idx], temp[high] = temp[high], temp[pivot_idx] # 4.
return recursion(temp[:high]) + [temp[high]] + recursion(temp[high+1:]) # 5.
return recursion(arr)
- 피벗을 선택합니다. 이 코드에서는 가장 앞에 위치한 값을 피벗으로 선택했습니다.
- 1번 값을 low, 마지막 값을 high로 설정하고 피벗보다 작은 경우 왼쪽으로, 피벗보다 큰 경우 오른쪽으로 이동합니다. low와 high값이 교차하는 순간 모든 값에 대한 피벗과 비교가 끝납니다.
- 2번에서 왼쪽에서 피벗보다 큰 경우와 오른쪽에서 피벗보다 큰 경우 서로 값을 교환(swap)합니다.
- 2번이 종료된 경우 high 위치의 값과 피벗을 교환(swap)합니다.
- 재귀적으로 왼쪽과 오른쪽을 다시 피벗을 설정하고 정렬을 시작합니다.
- 더이상 교체할 값이 없는 경우 종료합니다.
시간 복잡도
최선의 경우 아래와 이미지와 같아진다.

순환 호출의 깊이
레코드의 갯수가 n개라고 가정하고 n은 2의 제곱이라고 가정한다면, $2^3\rightarrow 2^2 \rightarrow 2^1 \rightarrow 2^0$식으로 전개가 된다. 이를 일반화하면 $n=2^k$가 되고 $k=log_2n$가 된다.
순환 호출 단계의 비교 연산
각 순환 호출에서는 해당 리스트의 전체와 비교해야한다. 위의 코드를 살펴보면 피벗값은 가장 처음으로 설정되고 이후 low와 high를 통해 모든 값을 비교하므로 n으로 연산할 수 있다.
따라서 퀵 정렬의 시간 복잡도는 $O(nlogn)$이다.
모든 정렬에서 이상적인 계산으로는 퀵정렬이 가장 빠르다. 하지만 퀵정렬은 최악의 경우 $O(n^2)$이 걸리는데 그 이유는 아래와 같다.
리스트가 계속 불균형하게 나누어지는 경우이다. 특히, 이미 정렬된 리스트에 대하여 퀵 정렬을 실행하는 경우이다.
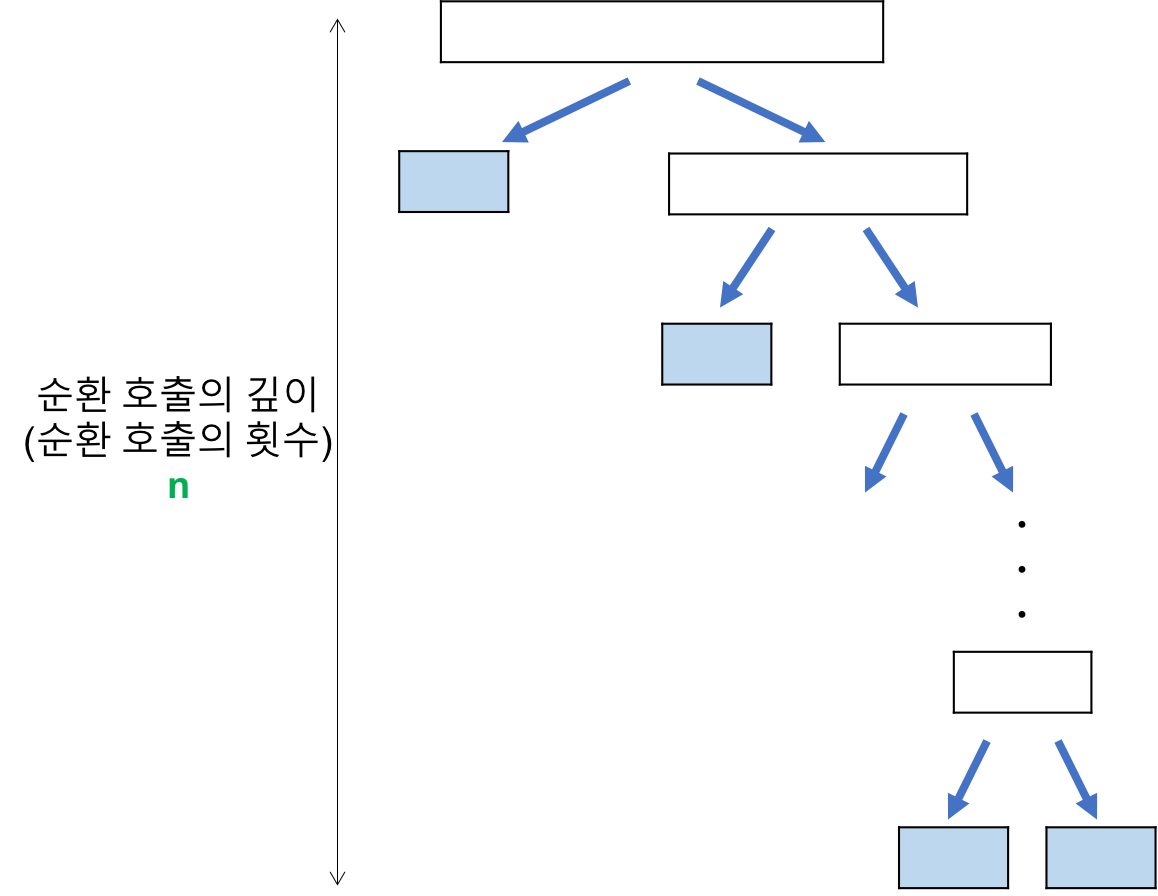
이런 경우 리스트의 깊이가 n번이 되므로 $O(n^2)$가 된다. 이를 해결하기 위한 방법으로는 피벗의 기준을 바꾸면 해결된다.
바꾸는 방식은 대표적으로 피벗의 기준을 가운데 값으로 하게 되면 항상 2 부분으로 나뉘게 되며 $log(n)$이 된다.
'cs 기초 공부 > 알고리즘' 카테고리의 다른 글
| 합병 정렬(Merge Sort) (0) | 2021.03.28 |
|---|---|
| 삽입 정렬(Insertion Sort) (0) | 2021.03.26 |
| 선택 정렬 (Selection Sort) (0) | 2021.03.26 |
| 정렬 기초 공부1 (Bubble Sort) (0) | 2021.03.25 |