Abstract
일반적인 방법으로 구현했을 때, 이 정렬은 안정 정렬(Stable Sort)에 속하며, 분할 정복 알고리즘의 하나입니다.
하나의 리스트를 두 개의 균등한 크기로 분할하고 분할된 부분 리스트를 정렬한 다음, 두 개의 정렬된 부분 리스트를 합하여 전체가 정렬된 리스트가 되게 하는 방법입니다.
- 분할(Divide) : 입력 배열을 같은 크기의 2개의 부분 배열로 분할한다.
- 정복(Conquer) : 부분 배열을 정렬한다. 부분 배열의 크기가 충분히 작지 않으면 순환 호출을 이용하여 다시 분할 정복 방법을 적용한다.
- 결합(Combine) : 정렬된 부분 배열들을 하나의 배열에 합병한다.
Process
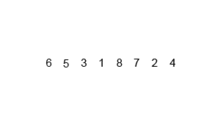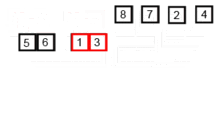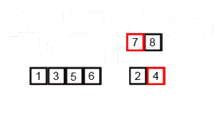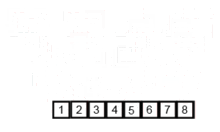
합병 정렬은 추가적인 리스트를 필요로 한다.
- 리스트의 길이가 0 또는 1이면 이미 정렬된 것으로 본다.
- 그렇지 않은 경우에는 정렬되지 않은 리스트를 절반으로 잘라 비슷한 크기의 두 부분 리스트로 나눈다.
- 각 부분 리스트를 재귀적으로 합병 정렬을 이용해 정렬한다.
- 두 부분 리스트를 다시 하나의 정렬된 리스트로 합병한다.
Python Code
def mergeSort(arr:list):
def recursion(arr:list):
if len(arr) == 1 or len(arr) == 0: # 1.
return arr
mid = len(arr) // 2
recursion_a = recursion(arr[:mid]) # 2.
recursion_b = recursion(arr[mid:])
idx_a = 0
idx_b = 0
temp = []
while idx_a < len(recursion_a) and idx_b < len(recursion_b): # 3.
if recursion_a[idx_a] < recursion_b[idx_b]:
temp.append(recursion_a[idx_a])
idx_a += 1
else:
temp.append(recursion_b[idx_b])
idx_b += 1
if idx_a == len(recursion_a):
temp += recursion_b[idx_b:]
else:
temp += recursion_a[idx_a:]
return temp
return recursion(arr)
시간 복잡도

레코드의 개수 n이 2의 거듭제곱이라고 가정($n=2^k)$했을 때, 깊이에 따라서 다음과 같다. $2^3 \rightarrow 2^2 \rightarrow 2^1 \rightarrow 2^0$ 순으로 줄어들게 된다. 이것을 일반화하게 되면 $n=2^k$가 되고 결국 $k=log_2(n)$ 라는 것을 알 수 있다.
합치는 연산을 계산해보면 배열의 크기가 $1 \rightarrow 2 \rightarrow 4 .... \rightarrow n$순으로 증가하여 일반화하면 최대 n번의 비교를 하게 된다.
따라서 깊이 $log(n)$과 합치는 연산 $n$을 곱하여 $nlog(n)$이 된다.
'cs 기초 공부 > 알고리즘' 카테고리의 다른 글
| 퀵 정렬(Quick Sort) (0) | 2021.03.28 |
|---|---|
| 삽입 정렬(Insertion Sort) (0) | 2021.03.26 |
| 선택 정렬 (Selection Sort) (0) | 2021.03.26 |
| 정렬 기초 공부1 (Bubble Sort) (0) | 2021.03.25 |